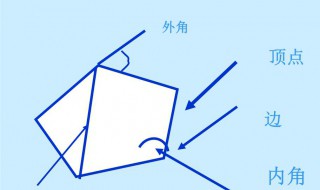
1、多边形的外角和是360度。
2、证明过程如下:设多边形的边数为n,则其内角和=(n-2)*180°,因为n边形有n个顶点,每个顶点的一个外角和相邻的内角互补,等于180°,所以n边形的外角和等于n*180°-(n-2)*180°等于360°,即n边形的外角和等于360度。
儿童教育2023-11-30 11:03:20未知

1、多边形的外角和是360度。
2、证明过程如下:设多边形的边数为n,则其内角和=(n-2)*180°,因为n边形有n个顶点,每个顶点的一个外角和相邻的内角互补,等于180°,所以n边形的外角和等于n*180°-(n-2)*180°等于360°,即n边形的外角和等于360度。
保护环境的优美句子 有关保护环境的句子