

学科竞赛是培养拔尖创新人才的重要途径,国家及地方对基础教育阶段的拔尖创新人才识别与培养越来越重视。
▶ 如何科学选拔信息学竞赛人才并搭建师生梯队,开展持续贯通的培养?
▶ 在竞赛训练过程中,不同发展阶段学习内容和学生能力的培养侧重及策略有哪些?
▶ 在具体信息学竞赛教学实践中如何对学生的计算思维、创造性思维等进行培养?
▶ 如何利用在线评测系统辅助竞赛训练,精准分析数据并结合学生自身的情况制订个性化策略,从而因材施教,让学生更加有效地进行信息学学习?
聚焦上述问题,广东省中山市中山纪念中学开展了一系列的研究与实践,系统分析和梳理了信息学竞赛生选拔和不同发展阶段的培养策略等,建立健全了行之有效的小初高信息学拔尖创新人才贯通培养机制,为信息学拔尖创新人才的选拔和培养机制的优化提供了理性认识和实践依据,从而更好地推动信息学竞赛活动的高质量发展。
拔尖创新人才的培养是建设创新型国家、实现中华民族伟大复兴的基础性、战略性工程。本文以“运动坐标”问题为例,介绍如何通过具体活动,发展学生的创造性思维,培养信息学拔尖创新人才。
慎思热议,发展学生独立思考、合作交流的能力
具有创造性思维的学生一定具备较强的独立思考能力,同时创新型人才也需具备合作交流的能力。在任何问题的解决过程中,既要给学生独立思考、解决问题的时间,又要组织讨论交流,形成多元的问题解决思路。
以“运动坐标”问题为例,题目的描述为:某动点在平面直角坐标系第一象限的整点上运动(含第一象限x,y轴上的整点),其运动规律为(x,y)(x+1,y+1)或(x,y)(x+1,y-1)。若该动点从原点出发,经过6步运动到(6,2)点,有多少种不同的轨迹。题目如图1所示。
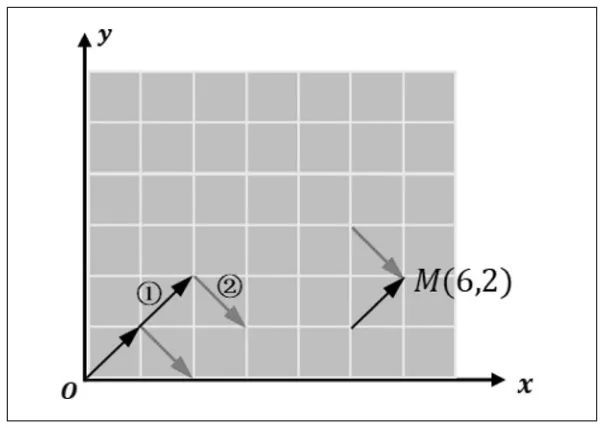
图1
1.缜密思考,精准分析
不管是具体的题目,还是生活中的问题,分析过程都体现了学生思维的缜密程度。在“运动坐标”问题中,动点有两种运动方式,其中每完成一次运动方式①,动点的横坐标和纵坐标都会增加1,每完成一次运动方式②,动点的横坐标增加1,而纵坐标减少1。
根据起点到终点坐标的变化,设运动方式①完成了a次,运动方式②完成了b次,动点从(0,0)到(6,2),横坐标增加了6,纵坐标增加了2。得到以下方程:
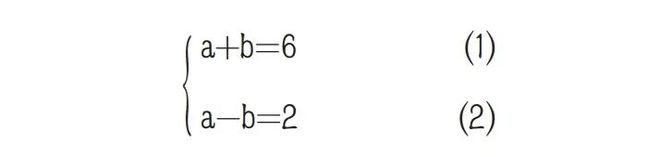
解得:a=4,b=2。即从(0,0)运动到(6,2),两种方式分别完成4次和2次。再结合象限约束,思考4次运动方式①和2次运动方式②有多少种可能。
这道题目对学生来说具有挑战性,可以让学生将他们分析问题的思维过程用精练的语言表述出来,从而培养学生既“精”又“准”地思考、分析与表述能力。
2.模拟验证,形象呈现
对于小数据量的问题,用图、表等形象化的方式启发学生的观察与思考,是一种常用的问题解决方法。针对“运动坐标”问题,教师可组织学生用图去模拟所有的解,并观察他们的模拟过程是否有序,是否有疏漏,并对模拟验证过程中逻辑有序的学生进行表扬。
模拟的过程可以由多名学生各绘一图,求同存异,也可以一人主讲,多人补充。通过以上两个步骤,学生在问题的思考、分析、讨论、交流中,学会独立思考、合作交流,既能将问题抽象概括,又能将抽象问题具象验证,创造性思维能力得到提升。
重构问题,发展学生基于已知探索未知的能力
创新创造不是凭空想象,很多时候是基于已有的知识、现象,去提出新的问题,探索不确定的事物与未知。针对“运动坐标”问题,教师可以和学生一起尝试将其重构成可以用程序解决、更大数据规模、有时间与空间限制的问题,并进行问题的辨析与解决。
下面是改编问题,时间限制为1秒,空间限制为256M。具体如下:某动点在平面直角坐标系第一象限的整点上运动(含第一象限x,y轴上的整点),其运动规律为(x,y)(x+1,y+1)或(x,y)(x+1,y-1)。给定终点(n,m),若该动点从原点出发,问动点从原点运动到终点,有多少种不同的轨迹?

引导学生开展发散性思考:问题中的数据规模再大一些怎么解决?问题一般化,没有具体的数字,而是改成n,m等一般性变量,该如何解决?改变题目的某个条件,解决方案要作何变化?
通过一系列的追问,引导学生深入思考题目的特点,从不同角度去寻找已知和未知之间的关系,重新构建问题的数学模型,再重新设计算法解决这个数学模型,最后通过程序来实现算法。这极大地锻炼了学生的思维能力,拓宽了思维的深度和广度,有利于形成发散性思维的品质,对学生创造性思维能力的培养有很好的效果。
一题多解,培养学生求同存异、探索最优的习惯
一题多解的思维习惯有助于激发学生的探究主动性与创新意识,在生生互动、师生互动的过程中,在对题目多样化解决方法的分享交流中,学生逐渐养成了求同存异又追寻“最优解”的习惯。以新题目的解法为例,通过师生交流,形成了搜索法、记忆化搜索、递推法、类卡特兰数等多种解法。下面介绍部分解法的关键分析。

为了便于理解搜索的原理,可以画出样例(6,2)对应的有别于之前模拟运动轨迹的搜索树(如图2),由结点和线条组成,展示了动点在执行某种运动方式后的位置变化。
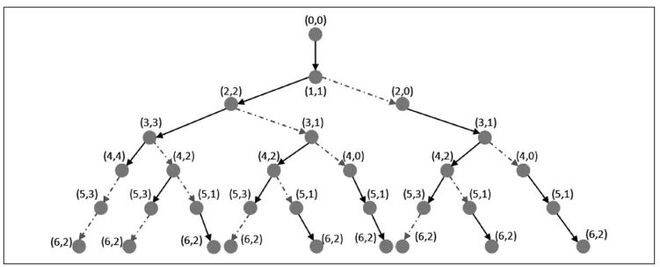
图2
其中结点(a,b)表示当前动点位置的横坐标为a,纵坐标为b,实线代表执行了运动方式①,虚线代表执行了运动方式②。从(0,0)到(6,2)的9种不同运动轨迹都可以在搜索树中找到。深度优先搜索的程序由于时间复杂度与运动轨迹数成正比,所以实际测试时只得到第一档数据的20分,对于第二、三档的数据测试结果显示超过时间限制。
方法二:记忆化搜索
方法一的程序之所以超时,原因在于搜索过程中出现了状态重复调用。分析得出程序慢的原因,就应引导学生思考如何解决该问题。本题可以定义F[i][j]表示从(i,j)到达终点(n,m)的运动轨迹数,也可以换一个方向,表示从(0,0)出发到达(i,j)的运动轨迹数,两种表示方法都是可行的,这里采用第二种方法。最终计算出F[n][m],就是问题的答案。
题目中已经保证了n≥m≥0且n,m奇偶性相同,根据方法一中对两种运动方式数量x,y的计算可知,问题一定有解。其中,当n=m=0时,F[0][0]=1。
当n>0时,F[n][m]的计算可以利用加法原理来完成,根据最后一步的运动轨迹分为以下两种情况:第一种情况,最后一步选择运动方式①,即从(n-1,m-1)运动到(n,m)。
经分析,这种情况存在方案的前提是n+m≥2且m>0,由于最后一步已确定,该情况的方案数等价于从(0,0)到(n-1,m-1)的方案数,即F[n-1][m-1]。第二种情况,最后一步选择运动方式②,即从(n-1,m+1)运动到(n,m)。这种情况存在的前提是n≥m+2,方案数等价于从(0,0)到(n-1,m+1)的方案数,即F[n-1][m+1]。

可以采用记忆化搜索来实现。首先把数组F初始化为-1,表示所有位置都未曾计算过,在调用递归函数dg(x,y)计算F[x][y]时,首先查看F[x][y]是否已经计算过,若已经计算过则直接返回F[x][y],若未计算过,则按照上面的递推关系式去计算,计算的结果再存回到F[x][y]处,以便下次需要计算F[x][y]时可以直接返回数组中的值,无需重复计算。
这样一来,每个点最多只会计算一次,时间复杂度为0(nm),大大提升了程序的效率。经过分析,学生编写的记忆化搜索程序最终获得了前两档数据的50分,对于第三档数据程序运行超时,且数组也开不到那么大,会超过空间限制。
结语
拔尖创新人才的培养非一朝一夕之功,创造性思维的培养要落实到每一次的教学实践中去,让学生在不断的分析讨论、重构问题、一题多解的迭代中发展创造性思维与创新能力。
(点击跳转至文章)
(点击跳转至文章)
信息学竞赛视角下培养计算思维的策略研究(点击跳转至文章)
基于在线评测系统的信息学竞赛精准化教学探讨(点击跳转至文章)
信息学竞赛教学中创造性思维培养的实践研究——以“运动坐标”问题为例
本文作者:
熊超
广东省中山市中山纪念中学
文章刊登于《中国信息技术教育》2023年第18期
引用请注明参考文献:
熊超.信息学竞赛教学中创造性思维培养的实践研究——以“运动坐标”问题为例[J].中国信息技术教育,2023(18):18-20.
欢迎订阅
纸质版订阅
电子版订阅





