数学里的假话,就是虚假的证明,也称为谬证。
如果谬证足够高级,一般人就很难看出到底哪里有问题,并且由此推导出错误的结论。|
接下来要介绍的就是证明 1 = 2的精彩的谬证。大家在阅读的时候,一定要思考一下到底错在哪里哦。
来源 | 《数学不只有一个答案:16个问题引发的头脑风暴》
作者 | [日]数学爱好者协会会长 一君
方法1 巧妙的变形
首先,看这个证明:
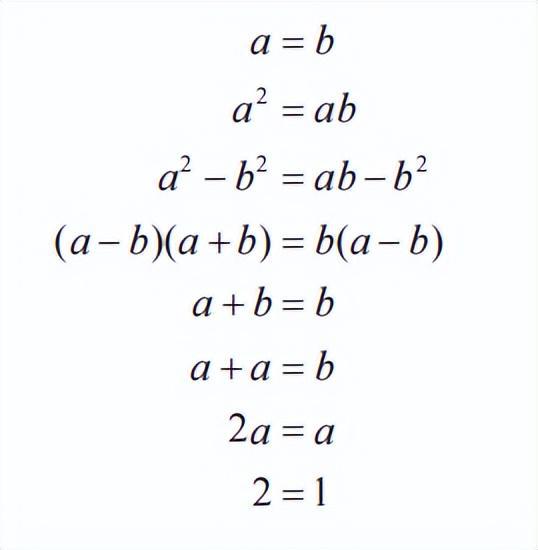
你能看出来这个证明错在哪里吗?
先尝试思考一下吧。
重点就在第 4 行和第 5 行之间。
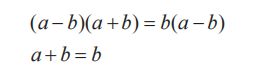
在这两行之间,我们对左右两边同时除以 a-b。
但在第 1 行已经定义了
a=b
因此 a -b =0,也就是说两边都除以 0,这就造成了后面计算结果的矛盾。
在数学中不能除以 0 是一条铁律,如果用计算器计算除以 0 就会出错。美国海军的宙斯盾巡洋舰所搭载的程序曾经因除以 0 的误操作发生系统瘫痪,导致主机宕机,在加勒比海上漂流了两小时。
在学校考试中,除以 0 也是要扣分的,
除以 0 真是全人类的公敌啊!
话说,为什么不能除以 0 呢?
假设 1÷0 的结果为 x,按照定义,除法是乘法的逆运算,原式就
可以变形为
由于任何数乘以 0 的结果都是 0,因此不存在乘以 0 的结果为 1
的数 x。当然,我们可以尝试强行定义 1=x×0。
于是有
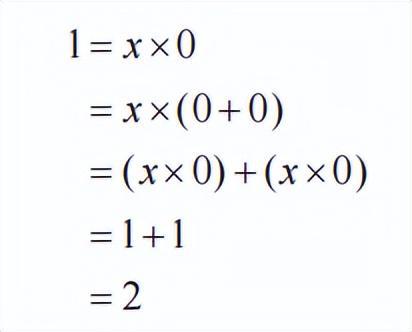
我们推出了 1=2 这种荒谬的结果。
如果将两边加 1,就可以将所有的正整数用等号连起来:
2=3, 3=4, 4=5, …
这真是个大危机啊!
这可太糟糕了,除以 0 好可怕。
方法2导数陷阱

两边同时求导,得
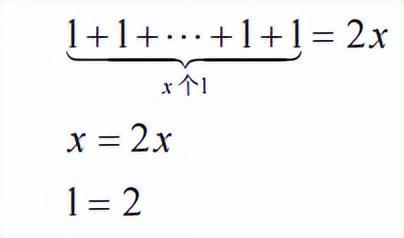
对函数 f(x)=x 求导,f'(x)=1;对 g(x)=x2 求导,g'(x)=2x。这样一想,感觉这个证明好像没什么问题。
虽然乍一看没问题,但这个把戏的秘密在于,左边的“x 个”被当成常量来处理了。
单纯把 x 的导数 1 相加 x 次是不行的,我们必须考虑到实际上“x个”中的 x 是个变量。
对函数求导就是求这个函数的斜率。“x 个 x”这样的函数画不出图像,也就不能对这个函数求导,因此这个证明是不成立的。

方法3视觉把戏
在以下边长为 1 的正三角形中,黑线的长度总和为 1+1=2。
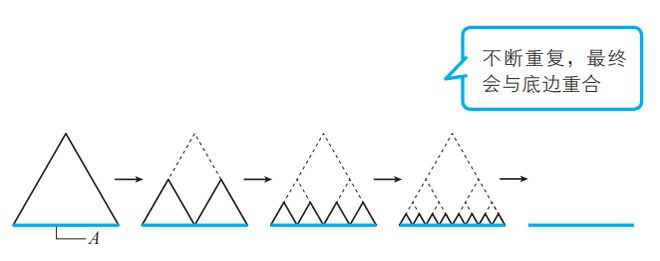
如上图所示,将正三角形的顶点向下翻转,翻转后黑线的长度总和仍然为 2。如此无限重复,最终会与蓝线 A 重合,而蓝线的长度为 1,因此 1=2。
怎么样,从直觉上看:
“咦?2 真的变成 1 了!”
有这种感觉的朋友应该不在少数吧?但其实这是错误的。尽管看上去黑线在不断接近蓝线 A,但实际上无论如何翻转,两条线都不会重合,因此 1=2 是不成立的。
同样,下面也是一个谬证。
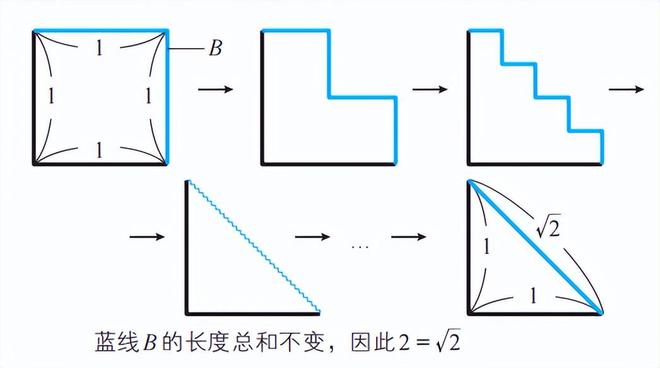
这个谬证是采用将正方形右上角向内侧翻转的方法构造的。
同样,在翻转过程中,蓝线 B 的长度总和始终是 2。不断翻转后会变成等腰直角三角形,两条直角边长度为 1,因此斜边长度为 √2,于是 2=√2 。
毋庸置疑,这是一个谬证,但是很容易让人感觉“看起来没错”,对吧?
真是名副其实的“视觉把戏”,是“大胆的假话”。
方法4不定积分陷阱
用分部积分法求下列积分:
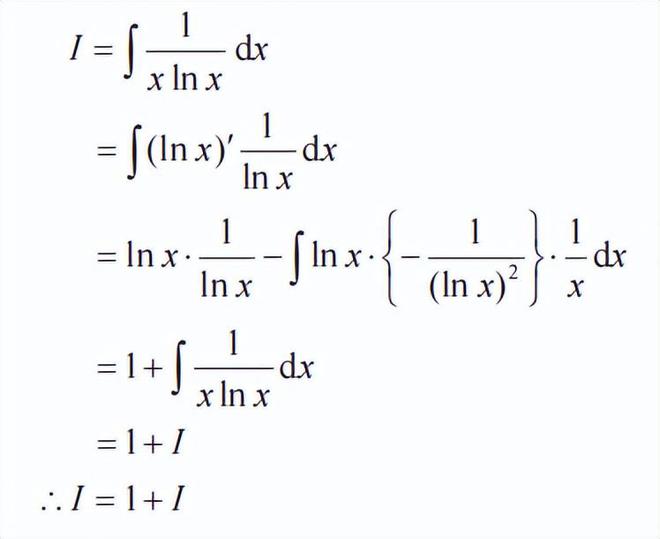
两边同时加上 1-I,得 1=2。
在这个证明过程中,遗漏了一个绝对不能遗漏的东西,因此才得出了 1=2 的错误结论。
在不定积分中绝对不能遗漏的东西,大家知道是什么吗?没错,那就是积分常数。
不定积分中包含一个潜在的常数差异,这个常数差异就用积分常数来表示。因此,在 I =1+I 这个等式中,I 本身包含了常数差异,尽管等式本身是正确的,但从两边同时减掉包含常数差异的 I 得到 1=2这一步是错误的。
使用 tan x 也可以变形为同样的形式:
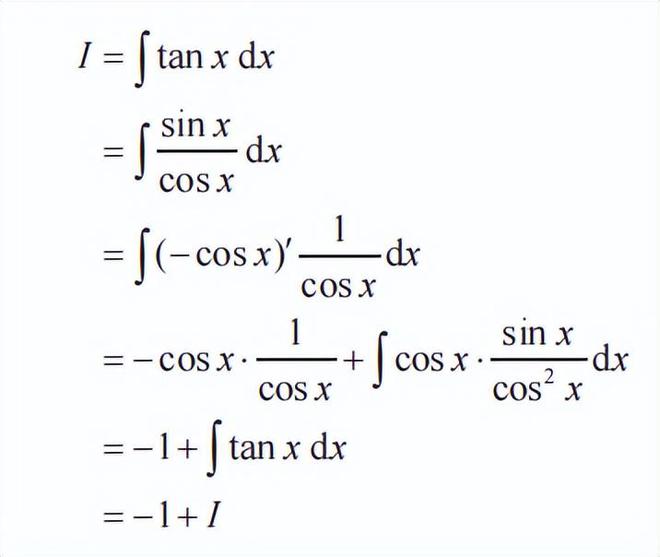
积分常数 C 因为存在感薄弱而经常被遗漏,某些情况下,这样的遗漏就会让我们推导出荒谬的结论。
大家可千万不要遗漏积分常数啊!
方法4交错级数
对于下列由整数的倒数交错加减构成的级数 A:
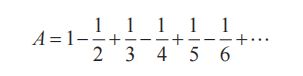
将各项的顺序重新排列得

因此 A=A/2,即 1=2。
这是一个难以反驳的谬证。
可能很多朋友会被这个证明迷惑。要指出这个证明的错误需要一些大学数学的知识。实际上,在数学上有这样一条规则,即“对于各项绝对值之和不收敛的级数,不能改变其各项的顺序”。
如果像这个谬证一样将无穷级数当成有限级数来处理,任意改变其各项的顺序,就会得出 1=2 这样的矛盾。
对于这样的解释,有些朋友可能感到不服气。事实上,18 世纪的数学家们在发现这条规则之前也对此感到非常苦恼。
大家只要将其理解为,我们平常计算的“有限项求和”中的规则不适用于“无穷项求和”就可以了。
在这里,级数 A 会收敛于 ln 2 这个有限的值,但 |A| 相当于调和级数,其值会发散为无穷大。因此,改变求和的顺序这种做法本身就是错误的。
话说,各项正负交替出现的级数称为交错级数。A 就是最有名的一个交错级数,称为墨卡托级数。

我们还可以反过来利用这一谬证:
假设 |A| 是收敛的,此时通过变形可推出 1=2,产生矛盾,因此根据反证法推出 |A| 是发散的。
如此即可证明 |A| 也就是调和级数是发散的。
在收敛的级数中,像 A 这样绝对值发散的级数称为条件收敛级数,而绝对值也收敛的级数称为绝对收敛级数。
总结一下,对于绝对收敛级数,即使改变各项的顺序,也会收敛到同一个值,但对于条件收敛级数,改变各项的顺序就会收敛到不同的值。
但这也并不完全是坏事。
因为存在这样一条浪漫的定理:“巧妙地改变条件收敛级数中各项的顺序(重排),即可使级数收敛于任意实数。”这条定理称为黎曼重排定理。
上文转自图灵新知,节选自《数学不只有一个答案:16个问题引发的头脑风暴》,[遇见数学]已获转发许可

数学不只有一个答案,数学追求的也不仅仅是答案。
试着从不同的角度和不同的难度来思考同一个数学问题,得到不同的思路和不同的解答,这样的大脑锻炼对提升数学思维和综合应用能力都大有裨益……关键是,这实在太有趣了!




